Math is Hard
Math is hard. I’ve never hated math back in school, but I also never did it, like, for fun. I did decent in college with the required math classes. As long as I payed attention, took lots of notes, and never missed a class, I was ok.
Coding is hard too. Front End Development is using code to put things on the screen, and make the things do things on the screen. Putting the things on the screen is the easy part. Making the things do things is when things get complex.
…
Ever since I completed the #100DaysOfCoding challenge, I’ve been struggling to find project ideas. I’ve been going back to the fundamentals and really digging deeply into JavaScript by reading books like Eloquent JavaScript and You Don’t Know JS. I started a React course on Udemy. I’ve been learning Node.js. The other day I watched a 4 hour Free Code Camp course on using Node.js with Express to start a server, using Graphql on the back end with Mongo, and React on the Front-End. I’ve definitely have learned a lot. But every time I attempt a project on my own, without having anyone to guide me, I struggle with the simplest things.
Take this App Ideas Collection repo. The first beginner project listed is a Binary to Decimal converter. I decide to give it a shot. I think to myself, “this should be simple enough. I know what’s a binary number. I can probably tackle this in an hour or so.” I decide no matter what, not to google any solutions. To really try it.
I start up a .js file with: let binaryNum = 1001; I stare at this one line. Ok so now what? So I google how how to make that conversion using plain old math. I find this:
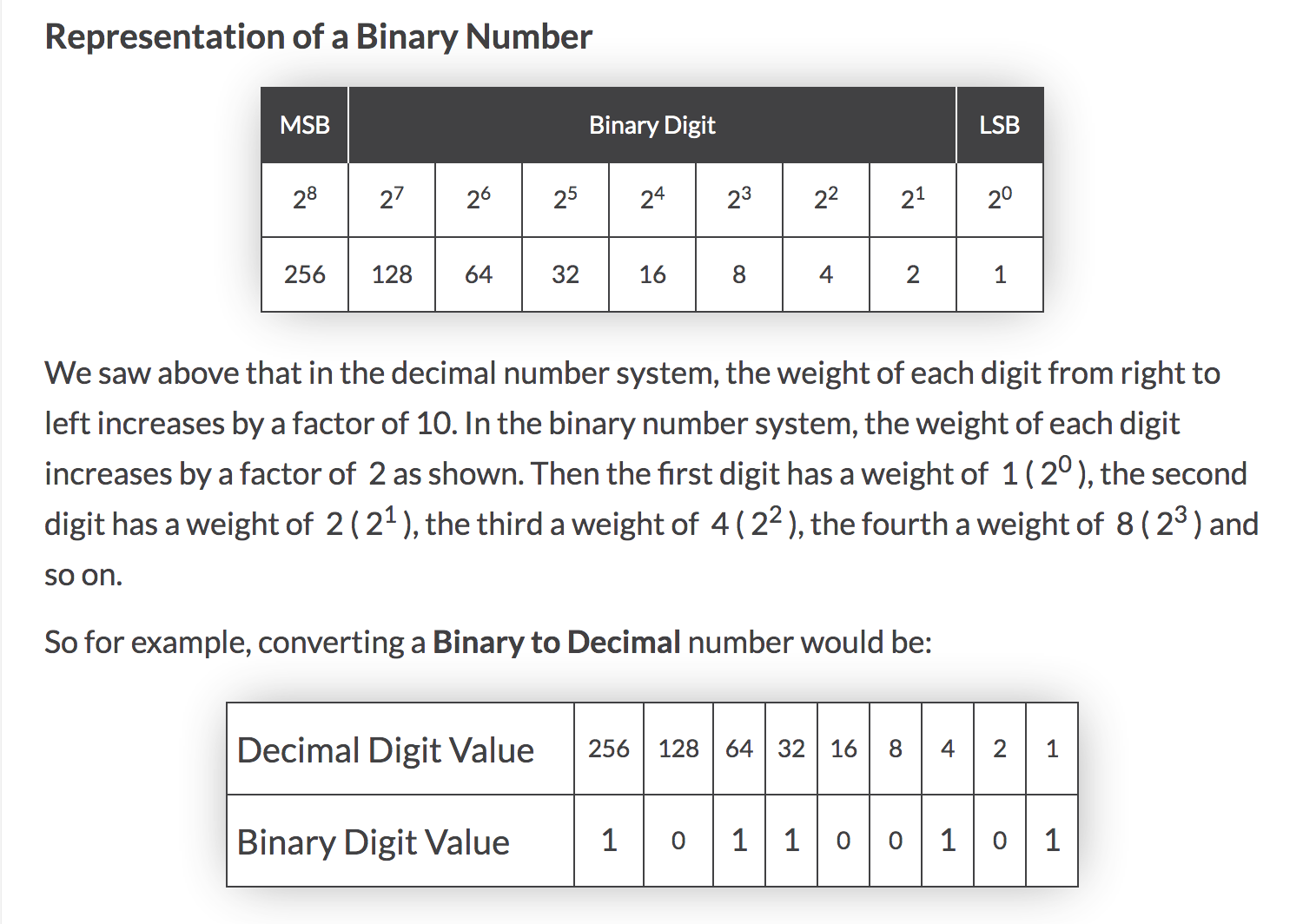
Ok so brain starts churning. I know I need a loop. The project has some constraints though and it says I can’t use an array. So I change the variable type to a string: let binaryNum = ‘1001’; Then I say: let positions = binaryNum.split; So wait? I just created an array of strings! [‘1’, ‘0’, ‘0’, ‘1’]. Hmmm, ok, so now what?
I read up some more on binary and the math formulas that help you convert them. I go through the conversion with a pencil and paper and really understand it. So I start doing things like:
function binaryConverter(positions) { Math.pow(positions[0], 2); … }
I gets late, my brain gets foggy. The next day I just click the example project link
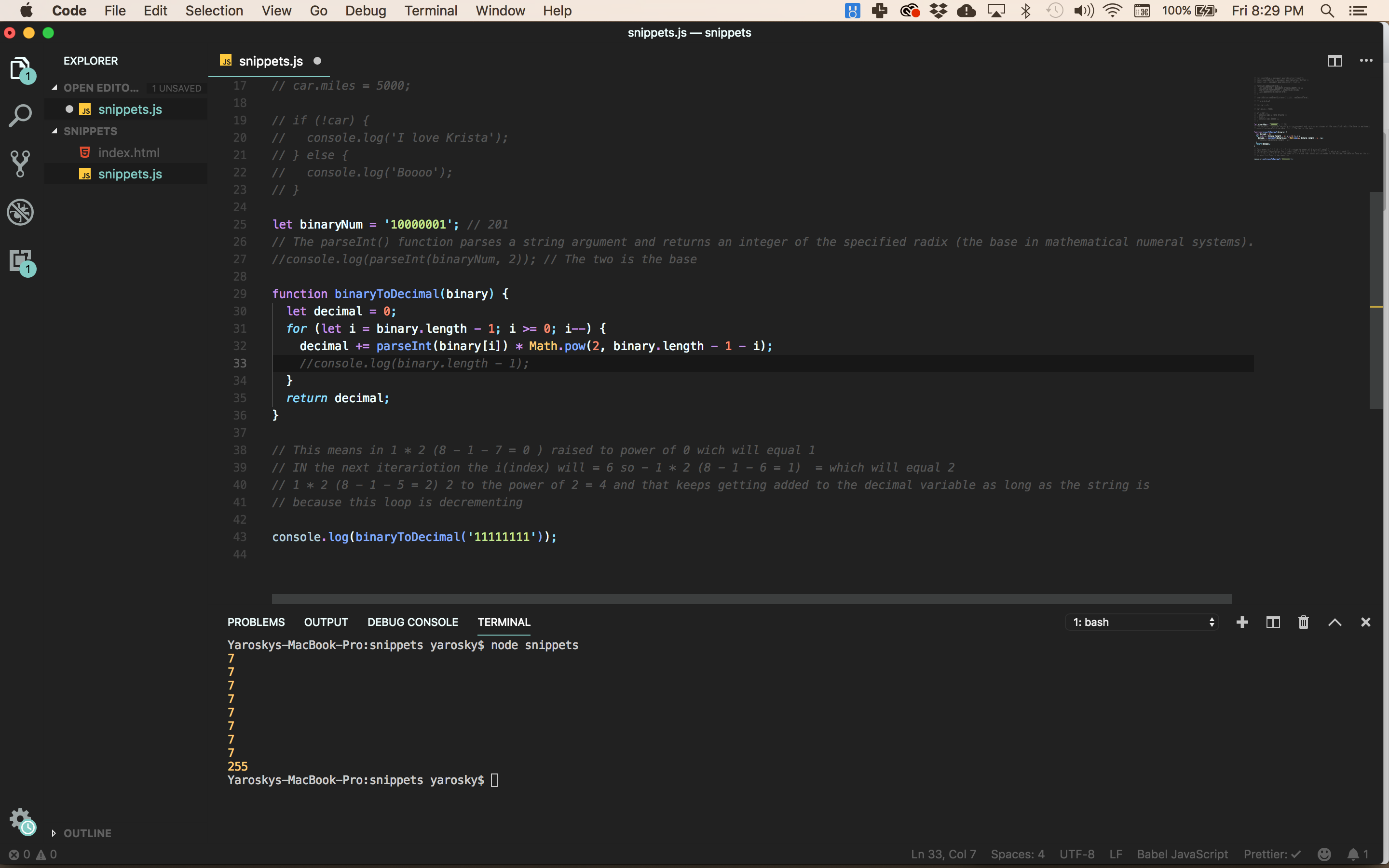
Here’s the thing. Even though I didn’t solve this by myself, I managed to understand everything that’s happening in the function. What that function is essentially doing is taking the string ‘11111111’ and doing this:
1 x 2 to power 7 = 128
1 x 2 to power 6 = 64
1 x 2 to power 5 = 32
1 x 2 to power 4 = 16
1 x 2 to power 3 = 8
1 x 2 to power 2 = 4
1 x 2 to power 1 = 2
1 x 2 to power 0 = 1
The result is 255.
Of course you can simply do parseInt(‘11111111’, 2) where the second argument here is the radix or base and does that whole thing in one fell swoop without having to use a for loop or Math.pow, but now I have a clear understanding on the logic here.
Let’s break this function down:
The function starts out by declaring the decimal variable starting at 0. It starts a for loop which is taking the binary.length - 1 which in the case of the string ‘11111111 means index 7 of that string. In other words, the binary.length for this string would be 8, but 8 - 1 = 7. So we are grabbing the 7th index position in this string which is the right-most 1. Now this - 1 thing on arrays and strings is clear to me! Instead of starting the the loop from left to right, it’s starting the loop from right to left. That’s also why i– is decrementing and the condition is testing if the the index is over or equal to zero and keeps subtracting until it reaches 0. Then we take the decimal value and do a += (7 times in this case) we parse the string as an integer with parseInt. The (binary[i]) x Math.pow(2, binary.length - 1 - i) is taking whatever value is in the index (binary[i]) (it’s going to be either 1 or 0) which in this case is 1 and multiply that by the result (8 - 1 - 7) = 0) 2^0 = 1. So you end up really with 1x2^0=1. But then on the next iteration of binary.length - 1 - i the index on the loop is 6 because it gets subtracted so on that iteration it’s (8 - 1 - 6 = 1) so this time it is 1x2^1=2. The arguments in the Math.pow function is saying: take 2, the first argument, and raise it the power of the second argument, in this case whatever the result of that calculation, binary.length - 1 - i
So it keeps doing that until it reaches zero and remember all these final results are being added at the same time with the decimal +=. So the first time the decimal is 0. So x = 0 + 1, then x = 1 + 2, then x = 3 + 4 and so on until everything adds up to 255 when i variable gets to 0.
Whoa! Hoping that this is helpful to someone.